How Do You Know if a Problem Is Lcm or Gcf

LCM and GCF

To observe either the To the lowest degree Common Multiple (LCM) or Greatest Common Factor (GCF) of 2 numbers, you always showtime out the same way: you discover the prime number factorizations of the two numbers.

Then (here's the play tricks!) you lot put the factors into a nice dandy grid of rows and columns, compare and dissimilarity, and then, from the table, take simply what you demand.

For instance:

• Find the GCF and LCM of 2940 and 3150.

Get-go, I demand to factor each of the numbers they've given me:

Content Continues Below

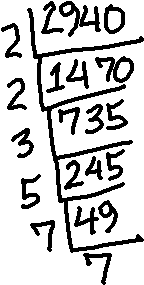
I started by dividing 2940 by the smallest prime that would fit into information technology, existence two. This left me with some other even number, 1470, so I divided by 2 once again. The result, 735, is divisible past 5, merely 3 divides in too, and it's smaller, so I divided past 3 to become 245. This is not divisible by 3 simply is divisible by 5, so I divided by v and got 49, which is divisible past 7.

At present I'll apply the aforementioned sequential-division process to 3150:

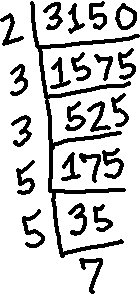
I've divided each of the given numbers by the smallest primes that fit into them, until I ended up with a prime result. The factorizations tin exist read from the numbers along the outside of the sequential divisions. So my prime factorizations are:

2940 = 2 × ii × 3 × five × 7 × 7

3150 = 2 × 3 × 3 × five × 5 × vii

I volition write these factors out, all nice and neat, with the factors lined upwards according to occurrance:

2940: two×2×3  ×v  ×seven×7 3150: 2  ×iii×3×5×5×7

This orderly listing, with each gene having its own cavalcade, will practice near of the work for me.

The Greatest Common Factor, the GCF, is the biggest ("greatest") number that will split up into (that is, the largest number that is a factor of) both 2940 and 3150. In other words, it'due south the number that contains all the factors common to both numbers. In this case, the GCF is the production of all the factors that 2940 and 3150 have in common.

Looking at the nice neat listing, I can run into that the numbers both have a factor of 2; 2940 has a second re-create of the cistron two, only 3150 does non, so I can simply count the one copy toward my GCF. The numbers also share one copy of 3, ane copy of 5, and one re-create of 7.

2940: 2×2×iii  ×v  ×seven×seven 3150: two  ×3×3×5×5×7 ----:----------------  GCF: two  ×3  ×5  ×7  = 210

Then the GCF is two × iii × 5 × vii = 210.

On the other manus, the Least Common Multiple, the LCM, is the smallest ("least") number that both 2940 and 3150 will divide into. That is, it is the smallest number that contains both 2940 and 3150 every bit factors, the smallest number that is a multiple of both these values; it is the multiple common to the ii values. Therefore, it volition be the smallest number that contains every factor in these two numbers.

Looking dorsum at the list, I see that 3150 has one copy of the cistron of 2; 2940 has 2 copies. Since the LCM must contain all factors of each number, the LCM must contain both copies of ii. However, to avoid overduplication, the LCM does not need three copies, because neither 2940 nor 3150 contains three copies.

---

This over-duplication event with factors frequently causes confusion, so let's spend a little actress time on this. Consider 2 smaller numbers, 4 and 8, and their LCM. The number iv factors equally ii × ii; eight factors as ii × 2 × 2. The LCM needs only have three copies of 2, in order to be divisible by both iv and 8. That is, the LCM is 8. You do not demand to have the three copies of ii from the 8, so throw in two extra copies from the four. This would give yous 32. While 32 is a common multiple, because iv and 8 both split evenly into 32, 32 is non the LEAST (smallest) mutual multiple, because you'd take over-duplicated the 2s when you threw in the extra copies from the 4.

Permit me stress again: let the squeamish neat list go on rail of things for yous, especially when the numbers get big. Returning to the exercise:

---

So, my LCM of 2940 and 3150 must comprise both copies of the gene 2. By the same reasoning, the LCM must incorporate both copies of iii, both copies of 5, and both copies of seven:

2940: ii×2×3  ×5  ×7×vii 3150: 2  ×three×iii×five×5×7 ----:----------------  LCM: two×2×3×iii×v×five×7×7 = 44,100

Then the LCM is 2 × 2 × 3 × 3 × 5 × v × vii × vii = 44,100.

Past using this "factor" method of listing the prime factors neatly in a table, you can e'er easily observe the LCM and GCF. Completely factor the numbers you are given, list the factors neatly with merely one factor for each cavalcade (you tin can accept 2s columns, 3s columns, etc, just a iii would never become in a 2southward column), then bear the needed factors down to the lesser row.

For the GCF, you comport down only those factors that all the listings share; for the LCM, you carry downward all the factors, regardless of how many or few values independent that factor in their listings.

---

Note: At that place is another method for finding LCMs and GCFs; it's chosen the "list" method. For case, to notice the LCM of iv and 6, you lot'd list their multiples, starting with the smallest and working your way up, until you establish the first duplicate. This get-go indistinguishable multiple would be your LCM:

4: four, viii, 12, xvi, xx, 24, 28, 32, ... vi: 6, 12, xviii, 24, 30, 36, ...

The first duplicate is 12, so this is the LCM.

But this "listing" method would be awful for big numbers like what we merely did above. Would you desire to try listing multiples for 2940 and 3150? I know I wouldn't. The process for GCFs tin can exist even more than painful! The factor method nosotros used above is much easier.

---

• Observe the LCM and GCF of 27, 90, and 84.

First, I demand to notice the prime factorizations:

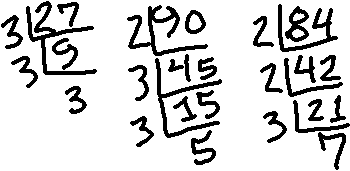
Then I will list these factorizations neatly:

              27:     3×3×3  90: 2  ×iii×3  ×v  84: 2×2×3      ×seven

Then the GCF (existence the production of the shared factors) and the LCM (being the product of all factors) are given by:

GCF:     three         = 3 ---:--------------  27:     3×iii×iii  90: 2  ×3×3  ×5  84: 2×ii×iii      ×7 ---:-------------- LCM: 2×2×3×3×3×five×7 = three,780

And then the GCF is 3 and the LCM is iii,780.

By the way, if yous prefer (or if you're lazy, similar me), you tin omit the "times" signs in your tables, and but listing the factors. Information technology'll look similar this:

• Find the GCF and LCM of 3, half dozen, and viii.

Get-go I gene the numbers and listing their prime factorizations:

Then my GCF and LCM are given by:

GCF:         = one ---:--------   3:       3   6: 2     3   8: 2 2 2 ---:-------- LCM: ii 2 2 three = 24

Notation that three, 6, and eight share no common factors. While 3 and vi share a factor, and half dozen and 8 share a cistron, at that place is no prime factor that all three of them share. Since ane divides into everything, then the greatest common factor in this instance is but 1. When i is the GCF, the numbers are said to be "relatively" prime; that is, they are prime number, relative to each other.

Then the GCF is 1 and the LCM is 2 × 2 × 2 × three = 24.

---

---

The GCF doesn't come up that much at this stage in mathematics, though some books employ it for factoring polynomial expressions by having the student find the GCF of all the terms in the polynomial and divide this value out of every term. Simply the LCM comes upwards every time you demand to find a common denominator for fractions. The cistron technique I demonstrated above works even for polynomial fractions. (The other method for finding the LCM, the "listing" method, will non piece of work for polynomials, which is why you need to acquire the cistron method.) If you need to find the LCM of 2 (or more) polynomials, y'all can do the exact same procedure as above:

• Find the LCM of x ³ + 5x ² + 6x and ii10 ⁱⁱⁱ + 4x ² .

Beginning I cistron the polynomials: x ^three + 510 ^two + 6x = ten(x ² + 5x + six) = 10(10 + ii)(ten + iii), and 2x ³ + 4x ² = 2x ^two(x + two). So I listing these factors out, nice and cracking:

And so the LCM is the product of one entry from each column:

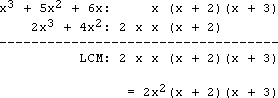
I have two copies of " 10 ", considering 210 ³ + 4x ⁱⁱ contains two copies. I don't demand iii copies of " x ", because neither polynomial contains three copies. I need only 1 copy of x + two, because neither polynomial contains more than just the one re-create. I need to account for the two from the second polynomial and the x + iii from the get-go polynomial.

The LCM is 2x ²(x + two)(10 + 3).

By the way, while you always multiply the factors together when you lot're finding the common denominators for regular fractions, you almost always want to go out the common denominators for polynomial fractions in factored course. That is, you'll need to multiply and simplify across the top, just don't multiply anything together across the bottom (in this case, don't multiply the x + 2 and the x + 3 to go x ^two + v10 + 6). Remember: you'll nonetheless need to try to reduce the polynomial fraction when you're done simplifying across the superlative, so you'll need the bottom in factored form in the end, anyway.

mcconnellbutragreake72.blogspot.com

Source: https://www.purplemath.com/modules/lcm_gcf.htm

Share this post